Oferujemy zajęcia z matematyki na poziomie podstawowym.
Od czego zależy sukces maturalny z matematyki?
Sukces maturalny zależy głównie od uporządkowania wiedzy, a czasami nawet od przyswojenia i zrozumienia treści programowych na nowo. Istotna rolę odgrywa sztuka logicznego myślenia, analizy i umiejętności argumentowania. Zadania sprawdzają bowiem, nie tylko rozumienie pojęć matematycznych, ale przede wszystkim dobieranie własnych strategii do rozwiązywania nietypowych problemów. To klucz do sukcesu, dzięki któremu staniecie się studentami takich kierunków jak rachunkowość i finanse, administracja, ekonomia itp. Matematyka jest jednym z trudniejszych przedmiotów maturalnych. Opanowanie tego przedmiotu wymaga dyscypliny, systematyczności i pokory.
Jak prowadzone są nasze zajęcia?
Matematyka to wiele działów, mniej lub bardziej rozbudowanych i skomplikowanych. Każde zajęcia rozpoczynają się od przypomnienia uczniom niezbędnych definicji i wzorów oraz innych zagadnień teoretycznych potrzebnych do rozwiązywania zadań egzaminacyjnych. Na podstawie pozyskanych informacji, uczniowie przystępują do rozwiązywania ćwiczeń wzorowanych na zadaniach egzaminacyjnych. Skupiamy się na praktycznym zastosowaniu wiedzy w charakterystycznych dla matury typów zadań otwartych i testowych. Zwracamy uwagę na najczęstsze problemy, najszybsze i najskuteczniejsze sposoby rozwiązywania zadań.
Nawet osoby, które przyszły do nas z minimalną wiedzą, są w stanie zdać maturę na dobrym poziomie, jeśli tylko w pełni wykorzystają możliwości oferowane im na naszym kursie.
Zajęcia na kursach maturalnych z matematyki prowadzone są w formie: wykładów, dyskusji, ćwiczeń, testów czyli mają charakter warsztatów ćwiczeniowych. W trakcie odbywanych kursów są przeprowadzane prace kontrolne, rozwiązywane arkusze maturalne, a także przeprowadzane próbne matury. Zakładamy także intensywną pracę własną kursantów w postaci zadań domowych, które później dokładnie omawiane są na zajęciach właściwych.
Nadzór merytoryczny nad naszymi kursami sprawuje Łódzki Kurator Oświaty, co jest gwarancją wysokich kwalifikacji, jak i doświadczenia zawodowego wykładowców oraz odpowiednio dobranych programów nauczania.
Główne cele naszych kursów:
- Powtórzenie, utrwalenie i rozszerzenie wiadomości zgodnie ze standardami wymagań egzaminacyjnych na danym poziomie.
- Ćwiczenie i rozwinięcie umiejętności wykorzystania zdobytej wiedzy poprzez rozwiązywanie zadań zamkniętych i otwartych typowych dla Nowej Matury.
- Kurs przeprowadzony będzie w oparciu o specjalnie opracowany program odzwierciedlający standardy wymagań egzaminacyjnych oraz zasady przeprowadzenia matury w roku 2024. Na kursie przekazujemy tylko przydatną wiedzę i ćwiczymy tylko niezbędne umiejętności, wykorzystujemy maksymalnie czas i stosujemy sprawdzone, najskuteczniejsze środki dydaktyczne.
Rozkład tematów na kursie z matematyki
| TEMATY LEKCJI | W zakresie TREŚCI PODSTAWOWYCH uczeń: | W zakresie TREŚCI ROZSZERZONYCH uczeń: | ILOŚĆ GODZ |
| LICZBY RZECZYWISTE | – Przedstawia liczby rzeczywiste w różnych postaciach – Oblicza wartości wyrażeń arytmetycznych – Posługuje się w obliczeniach pierwiastkami dowolnego stopnia i stosuje prawa działań na pierwiastkach – Oblicza potęgi o wykładnikach wymiernych i stosuje prawa działań na potęgach o wykładnikach wymiernych – Wykorzystuje definicję logarytmu i stosuje w obliczeniach wzory – Oblicza błąd bezwzględny i błąd względny przybliżenia – Posługuje się pojęciem przedziału liczbowego, zaznacza na osi liczbowej przedziały – Wykonuje obliczenia procentowe – Używa wzorów skróconego mnożenia na | – Stosuje definicję wartości bezwzględnej liczby rzeczywistej i jej własności w rozwiązywaniu zadań – Używa wzorów skróconego mnożenia. 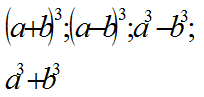 | 8 |
| FUNKCJE I ICH WŁASNOŚCI | – Podawać przykłady funkcji – Określać funkcję wzorem, tabelką, wykresem, grafem, opisem słownym – Określać z wykresu: – Dziedzinę funkcji, zbiór wartości funkcji, wartość funkcji mając dany argument, argument mając daną wartość funkcji, miejsca zerowe funkcji, przedziały monotoniczności funkcji, zbiór argumentów, dla których funkcja przyjmuje wartości dodatnie (ujemne), najmniejszą i największą wartość funkcji, wyznaczać dziedzinę funkcji określonej wzorem – Opisywać za pomocą funkcji zależności w przyrodzie, gospodarce i życiu codziennym – Interpretować zależności funkcyjne na podstawie danego wzoru – Na podstawie danego wykresu funkcji 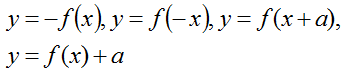 | – Przesuwa wykres funkcji o dany wektor – Zapisuje wzór funkcji otrzymanej w wyniku przesunięcia o dany wektor – Na podstawie danego wykresu funkcji: 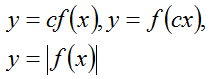 – Zapisuje wzór funkcji otrzymanej w wyniku danego przekształcenia | 6 |
| FUNKCJA LINIOWA I KWADRATOWA | – Rozwiązywać równania i nierówności liniowe z jedną niewiadomą – Określać liczbę rozwiązań równania liniowego z jedną niewiadomą – Rozwiązywać zadania tekstowe prowadzące do równań i nierówności liniowych z jedna niewiadomą – Rozwiązać algebraicznie i graficznie układy równań liniowych z dwiema niewiadomymi – Wyznaczać największą i najmniejszą wartość funkcji kwadratowej w przedziale – Wykorzystywać własności funkcji kwadratowej i jej wykresu do rozwiązywania zadań optymalizacyjnych – Rozwiązać równania i nierówności kwadratowe z jedną niewiadomą – Graficznie rozwiązywać równania i nierówności kwadratowe z jedną niewiadomą – Wykorzystuje własności funkcji liniowej i kwadratowej do interpretacji zagadnień geometrycznych, fizycznych itp. | – Rozwiązuje równania, nierówności i układy równań liniowych z wartością bezwzględną – Stosuje wzory Viete`a – Rozwiązuje równania i nierówności stopnia drugiego z wartością bezwzględną lub z parametrem – Rozwiązuje algebraicznie i graficznie układy równań z dwiema niewiadomymi, z których jedno może być stopnia drugiego | 8 |
| WIELOMIANY I FUNKCJE WYMIERNE | – Rozpoznawać wielomiany równe – Sprawdzać, czy liczba jest pierwiastkiem wielomianu – Rozkładać wielomian na czynniki – Rozwiązywać proste równania i wielomianowe – Określać dziedzinę wyrażenia wymiernego – Wykonywać działania na wyrażeniach wymiernych – Rozwiązywać proste równania wymierne – Szkicuje wykres funkcji | – Wykonuje dzielenie wielomianu przez dwumian – Rozkłada wielomian na czynniki – Dodaje, odejmuje i mnoży wielomiany – Wyznacza dziedzinę wyrażenia wymiernego z jedna zmienną – Wykonuje działania na wyrażeniach wymiernych – Rozwiązuje równania i nierówności wymierne | 6 |
| FUNKCJA WYKŁADNICZA I LOGARYTMICZNA | – Szkicuje wykresy funkcji wykładniczych dla różnych podstaw; – Posługuje się funkcjami wykładniczymi do opisu zjawisk fizycznych, chemicznych | – Szkicuje wykresy funkcji logarytmicznych dla różnych podstaw – Posługuje się funkcjami logarytmicznymi do opisu zjawisk fizycznych, chemicznych | 2 |
| TRYGONOMETRIA | – Wykorzystuje definicje i wyznacza wartości funkcji sinus, cosinus i tangens kątów o miarach od 00 do 1800 – Korzysta z przybliżonych wartości funkcji trygonometrycznych – Oblicza miarę kąta ostrego, dla której funkcja trygonometryczna przyjmuje daną wartość – Stosuje proste zależności między funkcjami trygonometrycznymi: 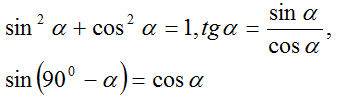 | – Stosuje miarę łukową i stopniową kąta – Szkicuje wykresy funkcji trygonometrycznych i na podstawie wykresu określać ich własności – Stosuje wzory na sinus i cosinus sumy i różnicy kątów, sumę i różnicę sinusów i cosinusów kątów – Rozwiązuje równania trygonometryczne | 6 |
| CIĄGI | – Wyznacza wyrazy ciągu określonego wzorem ogólnym – Bada, czy dany ciąg jest arytmetyczny lub geometryczny – Stosuje wzór na n-ty wyraz i na sumę n początkowych wyrazów ciągu arytmetycznego i geometrycznego | – Wyznacza wyrazy ciągu określonego wzorem rekurencyjnym – Oblicza granice ciągów – Rozpoznaje szeregi geometryczne zbieżne i oblicza ich sumy | 6 |
| GEOMETRIA ANALITYCZNA | – Wyznacza równanie prostej przechodzącej przez dwa punkty – Bada wzajemne położenie prostych przedstawionych w postaci kierunkowej – Graficznie przedstawia równania liniowe z dwiema niewiadomymi – Wyznacza odległość dwóch punktów – Znajduje obrazy figur geometrycznych w symetrii osiowej względem osi układu współrzędnych i symetrii środkowej względem początku układu współrzędnych | – Interpretuje graficznie nierówności liniowe z dwiema niewiadomymi oraz układy takich nierówności – Bada wzajemne położenie prostych przedstawionych w postaci ogólnej – Oblicza odległość punktu od prostej – Przedstawia okrąg I koło za pomocą równania z dwiema niewiadomym – Wyznacza punkty wspólne prostej i okręgu – Oblicza współrzędne oraz długość wektora | 6 |
| PLANIMETRIA | – Stosuje zależności między kątem środkowym i kątem wpisanym – Korzysta z własności stycznej do okręgu i własności okręgów stycznych – Rozpoznaje trójkąty podobne i wykorzystuje cechy podobieństwa trójkątów – Korzysta z własności funkcji trygonometrycznych | – Stosuje twierdzenie o kręgu wpisanym w czworokąt i okręgu opisanym na czworokącie – Stosuje twierdzenie Talesa i twierdzenie odwrotne do Talesa – Znajduje obrazy figur geometrycznych w jednokładności – Stosuje twierdzenie sinusów i cosinusów | 8 |
| STEROMETRIA | – Rozróżnia: wielościany i bryły obrotowe – Stosuje związki miarowe w bryłach z zastosowaniem trygonometrii – Określa jaką figurą jest dany przekrój prostopadłościanu płaszczyzną | – Określa, jaką figurą płaską jest dany przekrój graniastosłupa lub ostrosłupa płaszczyzną – Określa, jaką figura jest dany przekrój sfery płaszczyzną | 7 |
| ELEMENTY STATYSTYKI OPISOWEJ. TEORIA PRAWDOPODOBIEŃSTWA I KOMBINATORYKA | – Oblicza średnią ważoną i odchylenie standardowe zestawu danych – Zlicza obiekty w prostych sytuacjach kombinatorycznych – Oblicza prawdopodobieństwa stosując klasyczną definicję prawdopodobieństwa | – Wykorzystuje wzory na liczbę permutacji, kombinacji, wariacji i wariacji z powtórzeniami – Oblicza prawdopodobieństwo warunkowe – Korzysta z twierdzenia o prawdopodobieństwie całkowitym | 6 |
| RACHUNEK RÓŻNICZKOWY | – Oblicza granice funkcji – Oblicza pochodne funkcji wymiernych – Korzysta z geometrycznej i fizycznej interpretacji pochodnej – Korzysta z własności pochodnej do wyznaczania monotoniczności funkcji – Znajduje ekstrema funkcji wielomianowych i wymiernych – Stosuje pochodne do rozwiązywania zagadnień optymalizacyjnych | 6 | |
| ARKUSZE MATURALNE Poziom podstawowy. Poziom rozszerzony. | 10 | ||
| Próbny egzamin maturalny z matematyki. Poziom podstawowy. Poziom rozszerzony. | 3 | ||
| Omówienie próbnej matury z matematyki | 2 | ||
| UMIEJĘTNOŚCI | POZIOM PODSTAWOWY | POZIOM ROZSZERZONY |
| Wykorzystania i tworzenia informacji. | Interpretuje tekst matematyczny i formułuje uzyskane wyniki. | Używa języka matematycznego do opisu rozumowania i uzyskanych wyników. |
| Wykorzystania i interpretowania reprezentacji. | Używa prostych, dobrze znanych obiektów matematycznych. | Rozumie i interpretuje pojęcia matematyczne i operuje obiektami matematycznymi. |
| Modelowania matematycznego. | Dobiera model matematyczny do prostej sytuacji. | Buduje model matematyczny danej sytuacji, uwzględniając ograniczenia i zastrzeżenia. |
| Użycia i tworzenia strategii. | Stosuje strategię, która jasno wynika z treści zadania. | Tworzy strategię rozwiązania problemu. |
| Rozumowania i argumentacji. | Prowadzi proste rozumowanie, składające się z niewielkiej liczby kroków. | Tworzy łańcuch argumentów i uzasadnia jego poprawność. |
Gwarantujemy:
- Wysoko wykwalifikowanych wykładowców (nauczyciele po specjalnych kursach z uprawnieniami egzaminatorów),
- naukę w małych grupach,
- systematyczną ocenę postępów nauczania,
- próbny egzamin w trakcie kursu,
- zajęcia w centrum Łodzi,
- wysoką zdawalność,
- materiały dydaktyczne w cenie kursu.


